機械設計技術者試験の科目の一つである、応用総合のなかの「エアシリンダ 90°起伏装置」についての勉強資料を公開します。3D化していますが簡素なモデルのため、比率等で気になる点があるかと思いますがご了承ください。
また、貯水タンクのドレン蓋開閉部の計算と似ている部分があるため、参考にシマブロさんのブログのリンクを貼っておきます。併せて確認してみてください。
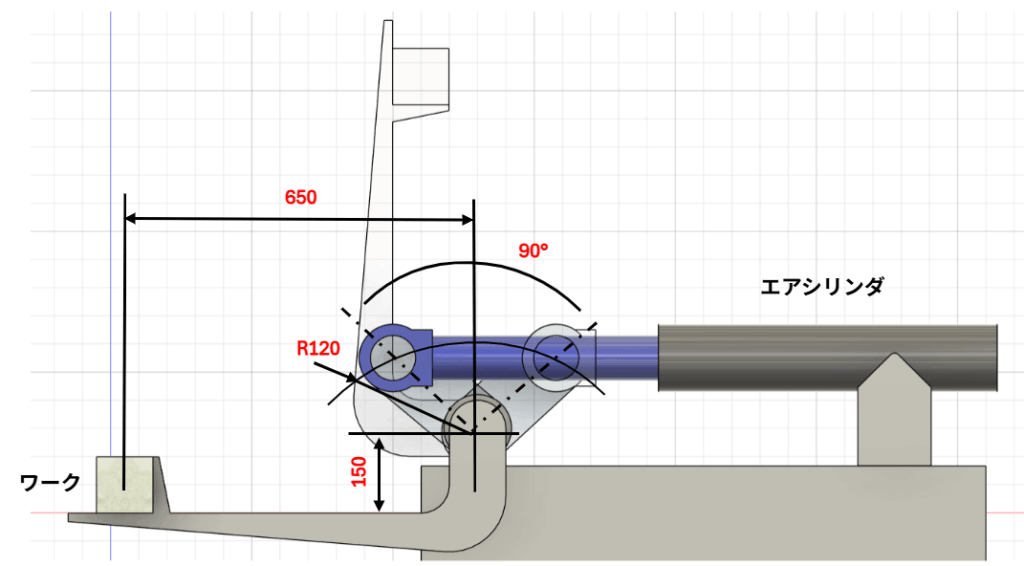
ワーク質量=30kg 安全率1.5 空気圧0.5MPa
(1)エアシリンダの必要最大の力
シリンダに必要な力
$$
\displaystyle
F = \frac{m \cdot g \cdot l}{R / \sqrt{2}} \; [\mathrm{N}] \
= \frac{30 \times 9.8 \times 650}{120 / \sqrt{2}} \
= 2252 \; [\mathrm{N}]
$$
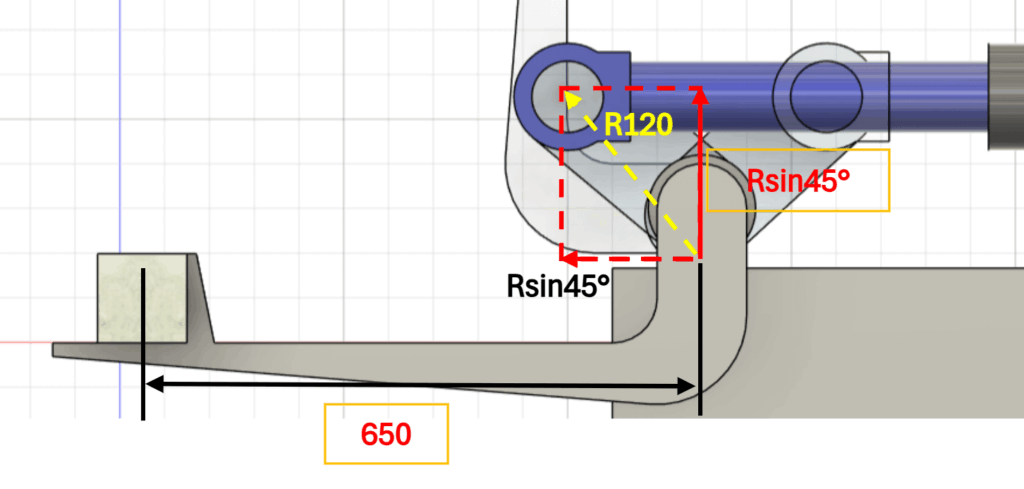
シリンダ径D
$$
D = \sqrt{\frac{4 \times 2252 \times 1.5}{\pi \times 0.5}} \
= 92.8 \ [\mathrm{mm}]
$$
シリンダφ100/φ30とする。
シリンダ径を求める式はよく出ます。私が1級を受験した際も出題されましたので、覚えておきましょう。
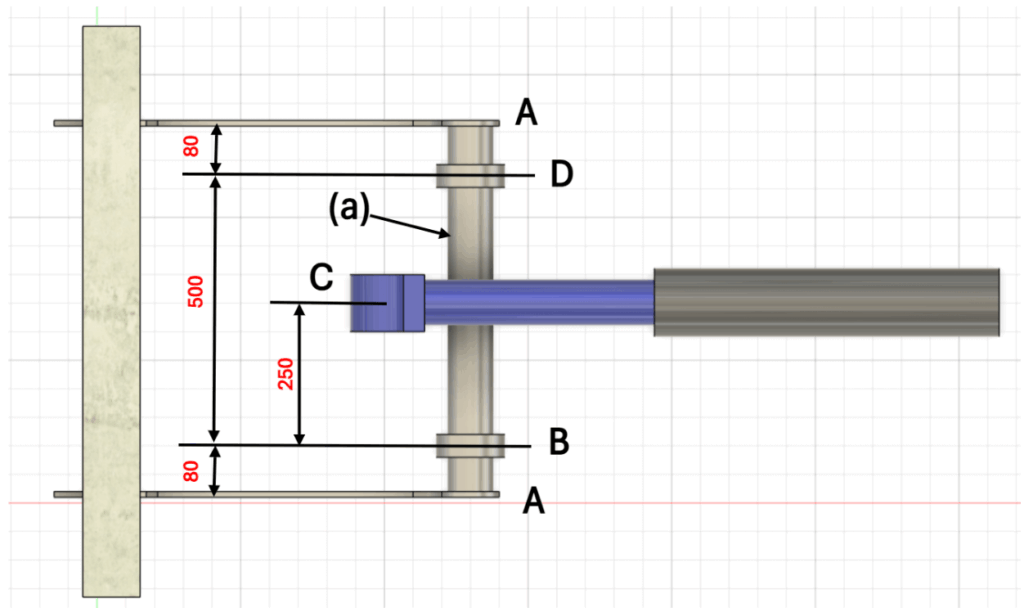
(2)ワーク質量が軸受BとDに加わる荷重
$$
V = \frac{m}{2} \times g \
= \frac{30}{2} \times 9.8 \
= 147 \ [\mathrm{N}]
$$
シリンダによる水平力を軸受けBとDで支持する。
$$
H = 2252 \times \frac{1}{2} \
= 1126 \ [\mathrm{N}]
$$
垂直荷重と水平荷重の合成 軸受に加わる最大荷重
$$
F_B = F_D = \sqrt{V^2 + H^2} \
= \sqrt{147^2 + 1126^2} \
= 1135 \ [\mathrm{N}]
$$
F=1135N
「最大」とつく場合、水平と垂直の合成荷重を算出する。
(3)ワーク質量による軸に加わる垂直方向モーメントB-D間
$$
M_v = \frac{m}{2} \times g \times l \
= \frac{30}{2} \times 9.8 \times 80 \
= 11760 \ [\mathrm{N \cdot mm}]
$$
シリンダによる水平方向モーメントC点が最大
$$
M_H = \frac{F \times l}{4} \
= \frac{2252 \times 500}{4} \
= 281500 \ [\mathrm{N \cdot mm}]
$$
合成による曲げモーメント
$$
M_\mathrm{max} = \sqrt{M_v^2 + M_H^2} = \sqrt{11760^2 + 281500^2} = 281635 \ [\mathrm{N \cdot mm}]
$$
ねじりモーメント
$$
M_f = \frac{m}{2} \times g \times L \
= \frac{30}{2} \times 9.8 \times 650 \
= 95550 \ [\mathrm{N \cdot mm}]
$$
出典:機械設計技術者試験2級







